Анонимные (lambda) функции

Автор: | Дата: 16 Сентябрь 2009 · 9 коммент. 

Когда я начинал работать с lisp'ом, я долго не мог понять смысла применения lambda-функций. И что это такое - достаточно долго для меня оставалось тайной (сказывался подход Visual Basic'a). На самом деле этот механизм очень удобен и прост.

Фактически lambda-функции - неименованные куски кода. Обычные функции, объявляемые в момент вызова, вычисляемые и после выхода из области видимости уничтожаемые.
Уже приводился элементарный код

1
(mapcar (function 1+) '(1 2 3))

Немного усложним его: допустим, в списке '(1 2 3) могут присутствовать не только целые числа, но и их строковые представления. Необходимо точно так же добавлять по 1 к каждому элементу списка.
К примеру, список '(1 2 3) заменяем на '(1 3 "6" 0 "-12"). Преобразовать строку в число несложно - функций (atoi) работает корректно. Со строками. При попытке передать ей не строку получим ошибку несоответствия типов.
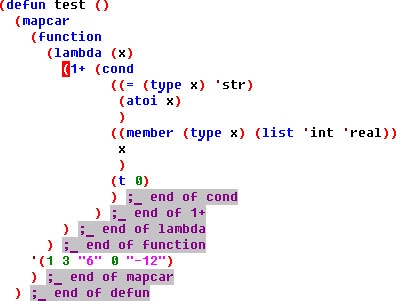
Я приведу сначала код, оформив его как функцию, например, test. А потом его разберу.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
(defun test ()
  (mapcar
    (function
      (lambda (x)
        (1+ (cond
              ((= (type x) 'str)
               (atoi x)
               )
((member (type x) (list 'int 'real))
x
)
) ;_ end of cond
) ;_ end of 1+
) ;_ end of lambda
) ;_ end of function
'(1 3 "6" 0 "-12")
) ;_ end of mapcar
) ;_ end of defun

Запустив VLIDE, создаем новый файл и вбиваем в этот новый пустой файл приведенный код.
Устанавливаем точку останова, как показано ниже.

Установить точку останова на открывающей скобке перед 1+

Установить точку останова на открывающей скобке перед 1+

Используя приводившиеся ранее клавиатурные сокращения, загружаем код в AutoCAD и в консоли VLIDE вызываем (test).
Код начнет выполняться, но тут же остановится. Просмотрев в окне Watch значение х, можно увидеть, что наша lambda-функция получила параметр, равный 1, выполнила расчеты и вернула 1+1=2. Выполняем следующий шаг, х=3; lambda-функция вернет 1+3=4. На третьем шаге х будет равен уже "6" (строке). lambda-функция в соответствии с (cond) выполняет преобразование х в число и прибавляет 1. Результат: 1+6=7.

Размещено в Код LISP, Функции LISP · Метки:



Комментарии

Есть 9 коммент. к “Анонимные (lambda) функции”
  1. Sleekka пишет:
    17 Сентябрь 2009 в 13:21

    При всем уважении, но смысл не раскрыт, показан только пример применения, то же самое можно было сделать в обычном цикле, смысл применения лямбда функций в том, что функция только однажды дифинируется в оперативной памяти что приводит к более высокой скорости работы программы, в сравнении с обычным циклом, потому как в цикле функция дифинируется каждый раз снова.
    http://ru.wikipedia.org/wiki/%D0%9B%D1%8F%D0%BC%D0%B1%D0%B4%D0%B0-%D0%B8%D1%81%D1%87%D0%B8%D1%81%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5

  2. Кулик Алексей aka kpblc пишет:
    17 Сентябрь 2009 в 14:53

    Проблемой было понять, что lambda - обычная, нормальная функция. Только анонимная. А пример сделан настолько примитивным сознательно: ну не хотелось мне ненужного усложнения, например, для vl-sort или vl-remove-if. Хотя сделать, конечно, не проблема. Если считаешь, что надо - можно и этот разбор добавить.

  3. ElpanovEvgeniy пишет:
    26 Сентябрь 2009 в 14:05

    Я согласен с Владимиром!

    Lambda функции, это абстракции второго порядка, по сравнению с обычными функциями!

    Для примера, напишем простую функцию:

    1
    (defun f (a) (1- (* a 2)))

    Если ее необходимо применить к списку, то код будет выглядеть:

    1
    (mapcar (function f) '(1 2 3 4))

    Здесь все отлично. Мы создали дополнительную абстракцию, которая на входе берет число, а на выходе возвращает результат вычислений ((Х * 2) - 1), где Х - наше число.
    Но, если мы будем использовать эту функцию только один раз, точнее, только для одного списка, то нам незачем регистрировать новую функцию и ее имя в документе. Вот здесь, нам и может понадобиться абстракция второго порядка - временная функция без имени. Из плюсов, более быстрая загрузка, меньший расход памяти, описание функции непосредственно в месте использования. Из минусов, не каждый сразу начинает понимать смысл и побаивается использовать...

    C использованием безымянной функции, этот код будет выглядеть:

    1
    (mapcar (function (lambda (a) (1- (* a 2)))) '(1 2 3 4))

    И еще, можно дать безымянной функции имя и потом многократно его использовать:

    1
    2
    3
    4
    (setq f (lambda (a) (1- (* a 2))))

    (mapcar (function f) '(1 2 3 4))
    (mapcar (function f) '(5 6 7 8))
  4. Do$ пишет:
    6 Октябрь 2009 в 15:06

    "b" и "d" в названии...

  5. Кулик Алексей aka kpblc пишет:
    8 Октябрь 2009 в 22:04

    Да, спасибо, исправляю :) Что значит привычка к быстрому завершению слова :)

  6. Михаил пишет:
    29 Апрель 2010 в 13:28

    Спасибо за обзор, только приступаю к изучению, очень все полезно. В общем еще раз большущее спасибо.

  7. Александр Токарев пишет:
    16 Сентябрь 2010 в 21:49

    Одно дополнение по лямбда-функции.

    Классикой использования лямбда-функции можно назвать так называемый лямбда-вызов в следующем формате:

    1
    ((lambda (<аргументы> [/ <локальные символы>]) <выражения>) <значения>)

    Вычисляется лямбда-вызов так (сам процесс называется лямбда-преобразованием):
    1) сначала аргументам присваиваются соответствующие значения, при этом количество значений должно быть равно количеству аргументов, иначе будет выдано сообщение об ошибке;
    2) затем вычисляются выражения лямбда-функции и возвращается результат вычисления самого последнего выражения.
    Заметим, что в выражении lambda-функции могут содержаться, как и в выражении именованной (defun) функции, локальные символы.

    К сожалению в справке ACAD по функциям AutoLISP и в наиболее известных книгах по AutoLISP, примеры с лямдба-вызовом не рассматриваются (как правило приводятся примеры её использования совместно с mapcar и apply).
    Мало того, в справочном описании функции обычно ошибочно утверждается, что она возвращает результат вычисления самого последнего выражения. Как было выше сказано, что этот результат возвращает лямбда-вызов.
    Сама же lambda-функция возвращает имя указателя lambda-функции наподобие следующего:

    1
    <#SUBR @09bc7118 -lambda->

    .
    В книгах по другим диалектам LISP лямбда-вызов рассмотрен достаточно подробно, например в знаменитом двухтомнике
    Э.Хювёнена и Й.Сеппеянена "Мир Лиспа" (том 1 стр.106-107).

    А теперь две иллюстрации:

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    ;;;Использование lambda-функции для нахождения факториала.
    ;;;В данном случае возвращается 479001600=12!.
    ((lambda (n)
       (repeat (car (setq n (list n 1)))
         (setq n (list (1- (car n)) (apply '* n)))
       )
       (cadr n)
     )
     ;;Целое число:
     12
    )
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    ;;;Использование lambda-вызова для нахождения периметра эллипса
    ;;;с известными полуосями (©Li6-D).
    ((lambda (a b / S)
       (setq S (mapcar 'abs (list a b)) a (apply 'max S) b (apply 'min S))
       (if (zerop b) (* 4 a)
         (progn
           (setq S (mapcar '* S S) b (list b (abs (apply '- S))) S (apply '+ S))
           (while (> (cadr b) 0)
             (setq b (list
                       (sqrt (* (car b) a))
                       (* 0.5 (1- (/ a (setq a (* 0.5 (+ a (car b)))))) (cadr b))
                     )
                   S (- S (cadr b))
           ) )
           (/ (* pi S) a)
     ) ) )
     ;;Длины полуосей эллипса:
     3
     5
    )
  8. Кулик Алексей aka kpblc пишет:
    16 Сентябрь 2010 в 22:38

    Спасибо :)

  9. Александр Токарев пишет:
    19 Сентябрь 2010 в 10:37

    Лямбда-вызов может быть вообще без аргументов:

    1
    ((lambda ([/ <локальные символы>]) <выражения>))

    Это похоже на выполнение нескольких выражений с помощью функции progn:

    1
    (progn <выражения>)

    С той разницей, что в лямбда-вызове можно объявить локальные символы, которые действуют только внутри тела (выражений) лямбда-вызова.

    Еще один пример, где лямдба-вызов без аргументов решает задачу квадратуры круга :) и возвращает число pi:

    1
    2
    3
    4
    5
    6
    7
    8
    9
    ((lambda (/ a b S) ;;Squaring the circle (©Li6-D)
       (setq a (sqrt 2) b '(1 . 1) S 3)
       (while (> (cdr b) 0)
         (setq b (cons (sqrt (* (car b) a))
                   (* 0.5 (1- (/ a (setq a (* 0.5 (+ a (car b)))))) (cdr b)))
               S (- S (cdr b))
       ) )
       (/ (* 2 a (car b)) (- S 2))
    ))

Поделитесь своим мнением


Я не робот.